Implied probability - what does it mean for novice bettors
At some point in your academic career, your math teacher more than likely used the term probability. The word probability referred to the likelihood of an event taking place. For instance, if a person was blindfolded, what are his/her chances of picking a specific object if there were four choices? In this example, the implied probability would be 1 out of 4 or 25 percent. Today, we will discuss the term implied probability as it relates to sports betting.
What is implied probability in sports betting?
Like the example provided above, implied probability in sports has a similar meaning. Implied probably refers to the overall likelihood of betting outcome as it pertains to the listed odds for a sporting event.
How does the implied probability calculator work?

To find out the implied probability of a sporting event, we must use a formula to convert the given odds into percentage form. Knowing the implied probability has a couple of benefits. 1) It helps bettors put odds into proper perspective. 2) Knowing the implied probability also helps bettors gain a better understanding of the various betting markets.
How to calculate the odds of winning?
In certain scenarios, the odds of winning are explicit. Like in the example of winning the lottery, the chances of a consumer purchasing the winning ticket are usually provided for the general public. This explains why the amounts can be several hundred thousand dollars.
In other situations, to calculate the odds of winning, we must know the total number of entries received during a specified time period. For instance, if you buy a raffle ticket, and the total number of tickets sold is 250. A person’s chances of winning can be broken down as follows:
Purchased tickets/Total number of tickets sold or 1/250. Your odds of purchasing the winning tickets are 1/250.
Converting odds to probability Excel equation
Calculating the probability of an event can seem like an overwhelming task. However, this is not the case when using a Microsoft Excel spreadsheet. The PROB function is used to determine the probability for an event or range of events, using the following syntax:
= PROB (x_range, prob_range, [lower_limit], [upper_limit])
X_Range: the range of values that shows different events.
Prob_range: the range of possibilities for each corresponding value in the x_range array.
Lower_limit: This is the lower limit value for which you want the probability.
Upper_limit: This is the upper limit value of an event for which you want the probability. It is important to remember that if this portion of the argument is ignored, then the calculation will determine only the probability associated with the value of the lower limit.
To calculate the probability in an Excel sheet, the user needs to enter the data into a table with two columns. The first column should be a range of numerical values. And their probabilities should be entered into the second column. Please note: the sum of all probabilities in the second column should be equal to 1 or 100%. You can check this by utilizing the SUM function in cell B12.
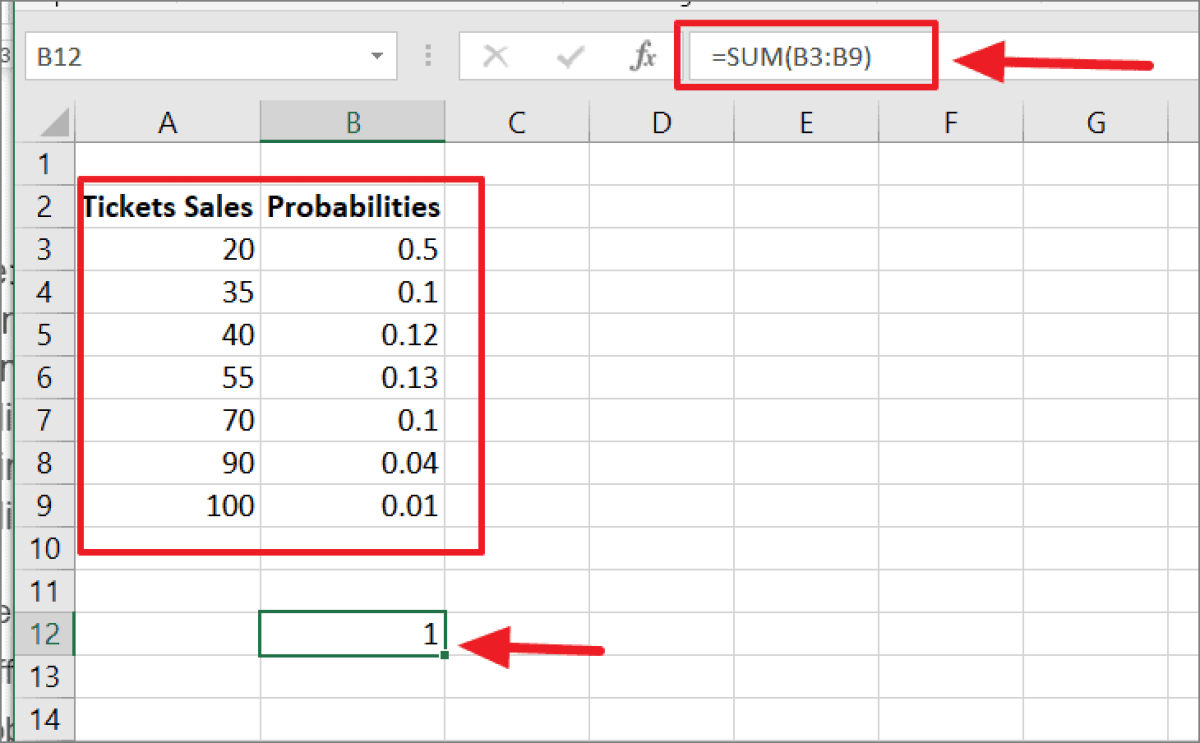
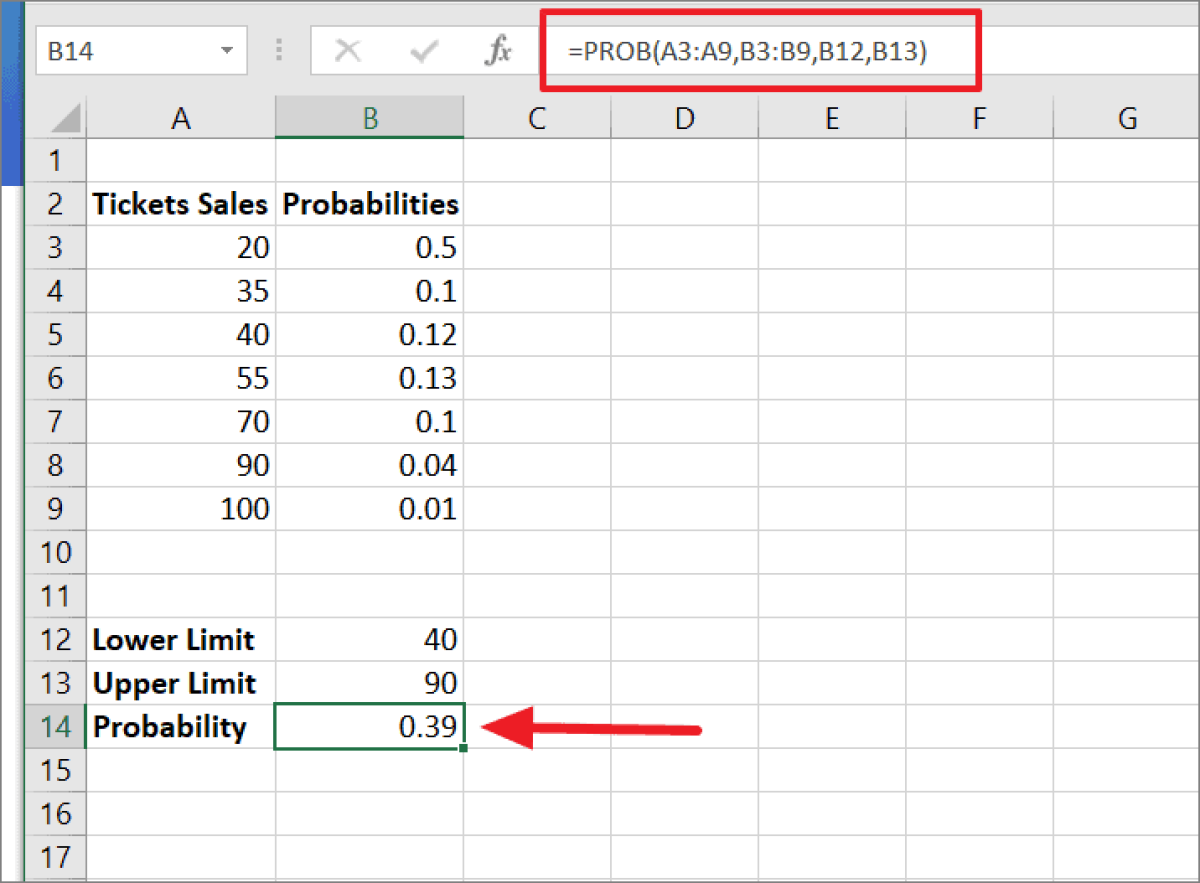
In this example, the lower and upper limit is set at 40 and 90, respectively. To calculate the probability here, you would use the formula =PROB (A3:A9,B3:B9,B12,B13).
A3:A9 represents the range of ticket sales. B3:B9 is the likelihood of getting sales quantity from column A. Cell B12 is the lower limit, while B13 represents the upper limit. The outcome of this calculation is .39 (or 39%) in cell B14. So, the probability of generating ticket sales between 40 and 90 is 39 percent.
How to convert American odds to implied probability
We will look at an example below in an NBA game between the New Orleans Pelicans and the Memphis Grizzlies.

In this scenario, the Grizzlies are 6.5-point favorites in a contest with the over/under set at 228.5 points. The Grizzlies are also heavy favorites from a Moneyline perspective. So, what are the Grizzlies’ odds of winning this contest?
This will be determined by taking the Moneyline odds for the game and substituting them into the formulas below.
Negative odds: Odds / (Odds + 100) *100 = Implied Probability
Positive odds: 100 / (Odds +100) * 100 = Implied Probability
Grizzlies -280: 280/ (280+100) *100 = 73.7%
Pelicans +220: 100/ (220+100) *100 = 31.3%
Because of the -280 odds, we already knew that Memphis is the favorite to win this game. And factoring in the implied probability helps us to put the bet into an even greater perspective. Based on the above calculations, the odds of Memphis winning this game is close to 74 percent.
Implied Probability Frequently Asked Questions
What is an implied probability?
An implied probability is a conversion of betting odds into a percentage. Implied probability considers the bookmaker margin to express the expected probability of an outcome taking place.
How do you calculate/use implied probability?
Implied probability is the likelihood of an outcome happening. Implied probability is calculated by dividing one by the decimal odds. For example, if a team has 2.50 odds to win a game, their implied probability of winning is 0.4 or 40%. This is the method bettors use to find the bets that have the most value.
What is good implied probability?
Good implied probability is when the expected/desired outcome has a high likelihood of occurring. For example, Moneyline odds that are -200 or greater. In this scenario, the implied probability is at least 66%. Moneyline odds that are between -150 and -199, the implied probability is at least 60%. Simply put, the teams with the higher Moneyline odds are expected to win that contest more times than not.
How do you calculate implied probability from Moneyline odds?
If a team has -200 Moneyline odds, the implied probability is calculated as follows. 200/(200+`100) 200/300 = .66 x 100 = 66%. So, the implied probability of a team with favored odds of -200, is 66 percent.
What does 30-1 odds mean in horse racing?
30-1 betting odds mean that out of 31 possible outcomes, the 30/1 odds are there will be 30 of one kind of outcome and 1 of another kind of outcome. The 30-1 odds mean that for every 31 betting events, your desired selection should win one time, and on 30 occasions, your desired selection will not win
Further Reading:
Our editorial content strives to be highly informative and educational to our audience, especially for visitors who are new or relatively new to analyzing and predicting sporting event results. All of our content is created by informed writers with backgrounds in their subject area and reviewed for omissions or mistakes.
Our editorial team is run by individuals with many years of experience in digital publishing, editorial, and content production. Our editorial content is always marked clearly in any instances where it may be sponsored by a third party, though it is still reviewed by our staff to ensure it remains consistent with our company mission.
- Popular
- Latest